Uncertainty Man - Werner Heisenberg

Werner Heisenberg was the winner of the 1932 Nobel Prize in Physics and the creator of the Heisenberg Uncertainty Principle in Quantum Mechanics. Here is a recording of an interview he gave in the 1970's at the Max Planck Institute in Munich, Germany, describing how the nature of quantum mechanics goes beyond the limit of descriptive language and challenges our common sense notions of understanding.

While a student of Amold Sommerfeld at Munich in the early 1920s Werner Heisenberg (1901-76) first met the Danish physicist Niels Bohr. He and Bohr went for long hikes in the mountains and discussed the failure of existing theories to account for the new experimental results on the quantum structure of matter. Following these discussions Heisenberg plunged into several months of intensive theoretical research but met with continual frustration. Finally, suffering from a severe attack of hay fever, he retreated to the treeless island of Helgoland. After days spent relaxing and swimming Heisenberg suddenly experienced the giddy sensation of looking down into the heart of nature and conceived the basis of the quantum theory. He took this theory to Bohr at Copenhagen, and for the next few weeks they argued and probed its implications long into the night. The results of these discussions became known as the 'Copenhagen interpretation of quantum theory' and are accepted by most physicists. Aspects of the interpretation include Heisenberg's uncertainty principle and Bohr's principle of complementarity.

Heisenberg is best known for formulating the uncertainty principle, a fundamental contribution to the development of quantum theory. This principle states that it is impossible to accurately measure simultaneously the position and momentum of a particle. 

In classical physics, we believe that we have full certainty of a system if we know the position and momentum of all particles at a given instant. When analyzing a system that consists of a single electron, Heisenberg imagined a theoretical configuration similar to the diagram on the left. This apparatus would be a gamma ray microscope that would try to determine precisely the position of the electron using high frequency photons. These high frequency photons would in turn interact with the electron to significantly alter its momentum. To try to determine the exact momentum we would then use lower energy photons, but this would alter minimally particle velocity hence giving us an overly "blurred" position.






In short, he found that there was no possible compromise that would allow us to accurately measure both variables. Generally, when a system is small enough, there is no physically possible to observe methods without significantly altering its state. The reason, returning to the example above, is because the photons used in the measurement are always quantised as photons and for a photon incident on a particle must have a peak wavelength corresponding to the diameter of the particle (otherwise the particle is transparent to photon) to interact. We know that the energy of a photon is inversely proportional to its wavelength, namely: 
E = hc/λ quantifies the maximum accuracy we can expect to get from an observation: the total error in our measurements simultaneous two conjugate variables will always at least equal to Planck's constant divided by a factor of 4 times pi  (3.141592654).  Planck's constant corresponds to the quantum of action, that is, the minimum action that can have on a system. Hence even with the most sensitive equipment, the laws of physics have a minimal amount of uncertainty given in units of Planck's constant. This is the origin of Heisenberg's Uncertainty Principle.

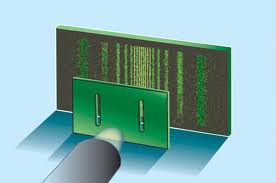
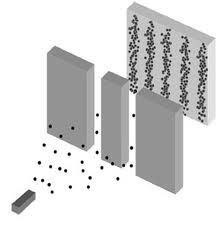
Another way to think about this is to also consider the famous double slit experiment. In this experiment, electrons, particles, enter a series of 2 slits and create an interference pattern just as if they are a wave. Even if the electrons are shot through one at a time, the path the electron traces out will cause it to interfere with itself. 

One way to interpret this view is that the double slitted sheet acts as a particle detector. Unlike a light wave, the electron wave is not a wave of electric and magnetic forces but is a probability wave. The particle, as a wave, has known momentum, propagating the wave packet paralell to the detector. However when it enters one or other of the slits its position becomes known. Hence we see the momentum vector of the wave become spread out over a continuum of directions. Therefore, we might think the uncertainty principle can be seen as a consequence of the wave view of particles alone, and can be derived from the familiar wave mechanics of light.

                                                             The Double-Slit Experiment. 

In the wave interpretation of particles, as the parallel probability wave of the electron propagates toward the detector we know its momentum (i.e. the Euclidean norm of the propagation vector) however its position is undefined in an infinity of possible positions along the wave peaks. When it enters either one of the slits its position is then known however the single momentum vector becomes blurred in an infinite number of projections and the wave then spreads out creating an interference pattern.

However ,there is more to the nature of quantum particles than they behave like waves some times but not others; as the great physicist Richard Feynman aptly put it "They behave in their own inimitable way, which technically could be called a quantum mechanical way. They behave in a way that is like nothing that you have seen before."

The path quantum particles takes is not always a straight line. Classical objects follow trajectories parallel to their momentum due to Hamilton's Principle of Least Action.

However, in quantum mechanics the Hamiltonian is quantised in units of Planck's constant. Once the position of the particle begins to reach the order of Planck's constant it will follow trajectories which deviate from the least action, i.e. a straight line trajectory. This explains more fully why particles appear to behave this way on the quantum scale rather than the macroscopic scale; there is no magical barrier to cross the classical to the quantum world, Planck's constant is small therefore quantum mechanics only behaves on small scales in space, time, energy and momentum.

(For a more detailed explanation of this see the notes section below and/or read Chapter 2 of Richard Feynman’s book, QED: The Strange Theory of Light and Matter, which uses this view to describe the behavior of photons)




To understand the uncertainty principle itself it is essential to reflect on the processes we call "observation" , or "measurement". When we make a measurement in an experiment, what we do is to try to extract information from a system by entering a meter that, by contact the observed system is altered by it. With the Uncertainty Principle it is clear that any act of measurement of a quantised system affects the system.
The uncertainty principle tells us that we can not simultaneously measure with infinite precision and a pair of conjugate variables. is, nothing prevents us to measure with infinite precision the position of a particle, but in doing so we have infinite uncertainty of its momentum over all possible time.


At that time Heisenberg first proposed this, there was general discussion among physicists about the possible ways to establish a coherent quantum theory, a coherent quantum mechanics. Among the many attempts, the most interesting for Heisenberg was the attempt of Hendrik Kramers to study the dispersion of atoms and, by doing so, to get some information about the amplitudes for the radiation of atoms. 

In this connection, it occurred to Heisenberg that in the mathematical scheme these amplitudes behaved like the elements of a mathematical quantity called a matrix. So, working with Kramers, they both tried to apply a mathematical calculus to the light dispersion experiments. The result of which was the expression for finding the cross-section for a photon scattered of an atomic electron.

The quantum mechanical derivation was given by Paul Dirac in 1927.

The scary formula above represents the probability of the emission of photons of energy  in the solid angle  (centred in the  direction), after the excitation of the system with photons of energy .  are the initial, intermediate and final states of the system with energy 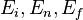 respectively; the delta function ensures the energy conservation during the whole process.  is the relevant transition operator.  is the instrinsic linewidth of the intermediate state.

The Kramers–Heisenberg formula was an important achievement when it was published, explaining the notion of stimulated emission, the necessary concept in the theory of lasers, and inelastic scattering - where the energy of the scattered photon may be larger or smaller than that of the incident photon - thereby anticipating the Raman effect.


From this it was clear that the first general quantum mechanical models describing the atom, turned out to be matrix mechanics. 

Although matrix mechanics agreed with experiments it was not a popular theory. Matrices may now be part of the mathematics that are taught to physics and chemistry students at universities in their first year, but in the 1920's few non-mathematicians had heard of them. Moreover they had an odd property. If two physical properties, say A and B, are multiplied with each other, one would expect AB=BA. If these properties are replaced by matrices, then this suddenly is not necessarily true.


Around that time, the first papers of Erwin Schrödinger became known. Schrödinger tried to develop the idea of wave-particle duality, first proposed by Louis de Broglie, into a new mathematical scheme, which was called wave mechanics. 

The famous Schrödinger Equation was actually able to treat the hydrogen atom on the basis of this wave mechanical scheme. This model was much more readily accepted then matrix mechanics, in part because the wave function could be visualized, and the theory was based on well-established classical mechanics.


The two conflicting notions of quantum mechanics, the matrix form of Heisenberg versus the wave form of Schrödinger meant that there was much disagreement between the two of them.

In fact the proponents of the matrix interpretation, Werner Heisenberg, Max Born and Niels Bohr blamed many widespread misconceptions about quantum mechanics on the popularity of the wave mechanics with little predictive power behind it.

Today, we usually use the terms "Schrödinger picture" and "Heisenberg picture" of quantum mechanics for the historical concepts wave mechanics and matrix mechanics, respectively.

Matrix mechanics and wave mechanics predict exactly the same results for experiments. This suggests that they are really different forms of a more general theory. In 1930 Paul Dirac showed that this is indeed the case. He gave a more general formulation of quantum mechanics; the one that is still used today in the form of Dirac's bra-ket notation for the wave function.

consisting of a left part, 〈φ|, called the bra, and a right part, |ψ〉, called the ket. 

The overlap expression 〈φ|ψ〉is typically interpreted as the probability amplitude for the state of the wavefunction ψ to collapse into the state ϕ.

Since bras and kets can be treated as row and column vectors respectively then it is understood that a bra next to a ket implies matrix multiplication. Hence the wave interpretation and matrix interpretation are equivalent and all of quantum physics follows from this.

In Dirac notation, the Schrödinger equation of time-evolution would be written as

H|ψ(t)> = iℏddt|ψ(t)>

where His the Hamiltonian operator. 


Heisenberg also developed the first models describing the role of electron spin in magnetization dynamics. The Heisenberg model for magnetism is an extension of the Ising model and is a statistical mechanical model used in the study of critical points and phase transitions of magnetic systems, in which the spins of the electrons in magnetic systems are treated quantum mechanically. 

The Heisenberg Model for magnetism, is given by the Heisenberg Hamiltonian: 
  
                                                  
where J is the exchange energy, and S represents a quantum spin operator. The summation is over nearest-neighbor spins; If J is positive, the spins Si and Sj tend to align ferromagnetically, If J is negative, the spins tend to allign anti-ferromagnetically.

This would be later extended into the Majumdar-Ghosh model and the Landau-Lifshitz model describing the quantum origins of magnetism in situations where the electron wavefunctions interact with each other in 1D, 2D and 3D.

Historically, when the Nazi government came to power in Germany, there was an innate distrust of what was vaguely called "Jewish Physics", some of which was the theoretical physics at the basis of quantum mechanics and relativity, due to the connections with Einstein and other famous Jewish physcisits. Some of Heisenberg's work came under scrutiny for this reason and vague though it was  the supporters of the equally vague termed "Aryan Physics" attacked Heisenberg. One attack was published in Das Schwarze Korps, the newspaper of the Schutzstaffel (SS), headed by Heinrich Himmler. In this, Heisenberg was called a "White Jew" who should be made to "disappear". These attacks were taken seriously, as Jews and many other groups of society were violently attacked, discriminated and often incarcerated even before the height of the Nazi reign of terror which came to its climax with the Holocaust which would have been known to many of the higher echelons in Nazi dominated society. Heisenberg had to fight back with an editorial and a letter to Himmler, in an attempt to resolve this matter and save himself from persecution and possible imprisonment.

Controversially of course, Heisenberg was in charge of the scientific research project of the German atomic bomb during World War II.  In 1939, shortly after the discovery of nuclear fission, the German nuclear energy project, also known as the Uranverein (Uranium Club), had begun. Heisenberg was one of the principal scientists leading research and development in the project.

This program started in April 1939, just months after the discovery of nuclear fission of Uranium in January 1939, but ended only months later, due to the German invasion of Poland, where many notable physicists were drafted into the army. However, the second effort began under the administrative auspices of the German army on the day World War II began (1 September 1939). 

From 15 to 22 September 1941, Heisenberg traveled to German-occupied Copenhagen with Carl Friedrich Freiherr von Weizsacker to lecture and discuss nuclear research and theoretical physics with his friend Niels Bohr. These meetings, revealed that Heisenberg and Weizsacker were reluctant to discuss the technical details of the German nuclear program outside of German soil, to do so would have been illegal. The meeting, which was said to have been dominated by Weizacker, was said to have been steered towars the discussion of fundamental nuclear physics, especially the process of the chain reaction in Uranium 238 rather than Uranium 235. This was said to a theoretical discussion, rather than an "intelligence gathering" mission on the development of weapons. 
It can be agreed that Heisenberg and Bohr were on good terms after these meetings and after the war itself was over. However, Bohr was genuinely shocked by Heisenberg's implications that Germany was in a secret race to develop a chain reaction in Uranium, considering the large technical effort that Heisenberg had said it required.
Even today there is much controversy whether or not it was Weizsacker or Heiseneberg who was responsible for convincing the Reich to begin a nuclear program and if Heisenberg was reluctant to build a nuclear weapon because he thought it would take too much time and resources or that his own work showed that a chain reaction would not yield a powerful blast. Documents relating to the Bohr-Heisenberg-Weizsacker meetings were released in 2002 by the Niels Bohr Archive and by the Heisenberg family.

On 26 February 1942, Heisenberg presented a lecture to Reich officials on energy acquisition from nuclear fission, after the Army withdrew most of its funding. The Uranium Club was transferred to the Reich Research Council (RFR) in July 1942. On 4 June 1942, Heisenberg was summoned to report to Albert Speer, Germany's Minister of Armaments, on the prospects for converting the Uranium Club's research toward developing nuclear weapons. During the meeting, Heisenberg told Speer that a bomb could not be built before 1945, and would require significant monetary and manpower resources.

The program eventually expanded into three main efforts: the Uranmaschine (nuclear reactor), uranium and heavy water production, and uranium isotope separation. Eventually an experimental nuclear pile called "Atomkellar" (literally "Atom cellar") was developed at the small town of Haigerloch, 40 miles from the university town of Tübingen, from late 1944 until April 1945 as the last large-scale test site for nuclear fission. 

                   The experimental reactor "Atomkellar" after the allied forces defeated Germany

During this time, a research group of the Kaiser Wilhelm Institute for Physics in Berlin, including Werner Heisenberg and Carl Friedrich von Weizsäcker were testing the development of a nuclear reactor with uranium and heavy water as moderator.

When Germany was invaded by the allied forces, Heisenberg had been captured and arrested by Colonel Pash at Heisenberg's retreat in Urfeld, on 3 May 1945, in what was a true alpine-type operation in territory still under control by German forces. He was taken to Heidelberg, where, on the 7th of May, Germany surrendered. Heisenberg did not see his family again for eight months. Heisenberg was moved across France and Belgium and flown to England on 3 July 1945.

Heisenberg was one of ten German scientists were held at Farm Hall in England. The facility had been a safe house of the British foreign intelligence MI6. During their detention, their conversations were recorded. Conversations thought to be of intelligence value were transcribed and translated into English. The transcripts were released in 1992. Bernstein has published an annotated version of the transcripts in his book Hitler's Uranium Club: The Secret Recordings at Farm Hall, along with an introduction to put them in perspective. A complete, unedited publication of the British version of the reports appeared as Operation Epsilon: The Farm Hall Transcripts, which was published in 1993 by the Institute of Physics in Bristol and by the University of California Press in the US

After the war was over, Heisenberg was free to go back to Germany as government, society and infrastructure was rebuilt. Before the war he was the director of the Kaiser Wilhelm Institute for Physical Chemistry at Göttingen (1941-1945) and went back there in 1946 after it was renamed the Max Planck Institute of Physics. He stayed there until 1958, after which he became the professor of Physics at the University of Munich where he remained until his death in 1976.

Heisenberg, like Bohr, also had meetings with Einstein, weeks before he passed away, and how even then Einstein disliked the idea of quantum mechanics for its inherent uncertainty, although he accepted that quantum mechanics had been rigorously verified through hundreds of experiments. Niels Bohr, who worked closely with Heisenberg was the one who heard Einstein say "God does not play dice", to which Bohr replie "Stop telling God what to do!". 

In essence, Einstein's view of quantum mechanics was not of hatred, merely discomfort that the subatomic world is not fully determinable and filled with uncertainty. Einstein did not trust Heisenberg's Uncertainty Principle as a way to describe the universe. However, Heisenberg did think extremely highly of Einstein's theory of special relativity, despite it being nearly outlawed by the Nazi's. Conversely, if "Jewish physics" had actually been banned in Nazi Germany, it would have been extremely bad for Heisenberg and colleagues working on Uranium fission. Therefore, under great personal risk, Heisenberg was willing to put his own safety on hold to discover the truth and would not have cared, in the same way Einstein would have, if the laws of physics seem displeasing.
By knowing that the uncertainty is inherent, Heisenberg was certain that the behaviour of quantum particles is based on probability and statistics and that these give us the power to go beyond classical thinking, something which continues to drive physics into the great unknown.

NOTES:

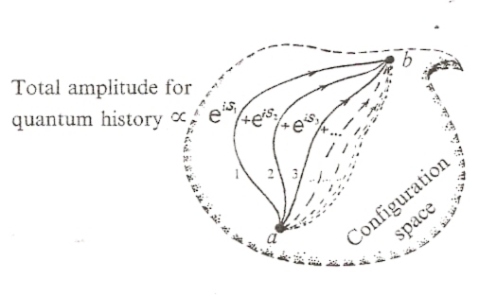
In quantum theory, the action, S,  is utilized to calculate a quantum amplitude. The basic idea is the sum over all possible paths. In any kind of phase space of dynamical variables we want to consider, the configuration state of any possible system is represented in terms of those dynamical variables. The quantum amplitude that describes the dynamical evolution of any system from one configuration state to another configuration state is defined by a sum over all possible paths that connect those initial and final configuration states:

Each path is weighted with a probability factor ψ that depends on the action S for that path as 

                                                           ψ=exp(2πiS/h)

The total quantum amplitude is a sum over all possible paths, and is understood in the sense of quantum probability. The probability factor ψ for any given path gives the quantum probability that the system will actually follow that particular path. The total quantum amplitude represents a quantum state of potentiality. In actuality, the system actually follows a particular path. The likelihood that the system will actually follow a particular path is determined by the probability factor ψ for that particular path, which depends on the action for that path.

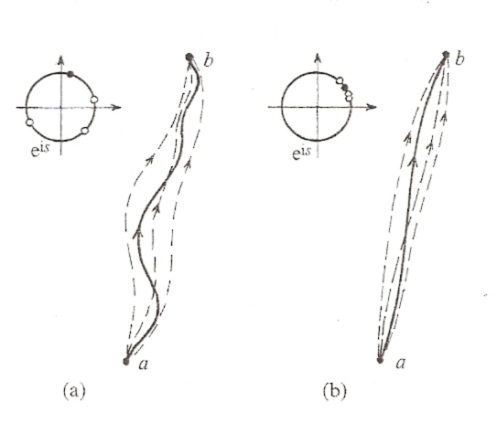
The most likely path in the sense of quantum probability is the path of least action. In some sense, the path of least action is like the path of maximal phase reinforcement in an interference pattern. When the waves are in phase with each other they tend to add together, and when the waves are out of phase with each other they tend to cancel out:

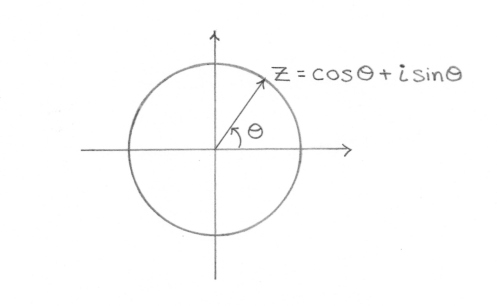
This phenomenon occurs in the total quantum amplitude since each probability factor ψ behaves like a wave. This phenomenon is inherently related to the nature of the complex plane, where the complex number z=exp(iθ)=cos(θ)+isin(θ) acts like a unit vector with a phase angle θ in the complex plane:

Euler's Equation can then be used to establish the fundamental relationship between the trigonometric functions and the complex exponential function. Euler's formula states that, for any real number x:

where e is the base of the natural logarithm, i is the imaginary unit, and cos and sin are the trigonometric functions cosine and sine respectively, with the argument x given in radians. 

The path of least action arises since the unit vector, z, tend to cancel out when the phase angles are out of phase with each other, and the vectors tend to add together when the phase angles are in phase with each other:

The path of least action is the most likely path in the sense of quantum probability. In actuality the system actually follows some particular path. In the case of a single photon in the double slit experiment, the photon acts like a particle that follows some actual path. The most likely path is the path of least action, but when we superimpose the behavior of many different individual photons we discover the interference pattern:

In the sense of quantum theory, every event is a decision point where the quantum state of potentiality branches into all possible paths.

Remember that since each particle path is weighted by the probability factor ψ, which is scaled by Planck's constant h, for amplitudes summed up over configuration spaces where Planck's constant becomes negligible the deviation from the least action (dS=0, i.e. a straight line) will become equally negligible. Hence we do not see quantum behavior in macroscopic configuration spaces, which is in everyday, ordinary, incoherent matter. 

SILEX Process -Top Secret Laser Enrichment Process Revealed

Photo Credit: Lawrence Livermore National Laboratory

Introduction to Laser Enrichment of Isotopes

Laser enrichment began in the mid-60’s for the purpose of separating isotopes of elements by the process of selective ionization by lasers. This process was designed to produce higher concentrations of specific desired isotopes of a chemical element by removing them from other isotopes that are not of use. The most popular and developed work has been performed on natural uranium. This process is a large contributor to the nuclear power industry and weapon development. Using the unique frequencies which atoms vibrate in gaseous form, a laser tuned to the vibrational frequency of a U-235 atom can cause the isotope to behave differently from the heavier U-238 atom to allow harvesting. However, technical difficulties have impeded translation from the laboratory to the commercial or weapons settings despite the efforts of more than a dozen countries since the 1970s.

Discovery

Laser enrichment was based around the early work coming from the 1970’s like MLIS (molecular laser isotope separation) and AVLIS (atomic vapor laser isotope separation). These two early discoveries in laser enrichment were both transferred into the United States Enrichment Corporation. The latter of the two earlier developments used tunable dye lasers which were able to make 235-Uranium absorb the photons and undergo excitation. The ions were then electostatically deflected into a collector while the unwanted was passed through. [ref 1].

Different Elements

1.Uranium- Laser enrichment of uranium is the most common application of laser enrichment and will discussed in detail below. This process separates isotopes for use nuclear fuel and energy production, and is much more useful and space efficient than older methods of uranium enrichment.

2.Carbon- Laser enriched carbon has applications in development of semiconductor material and biomedicine. The enriched Carbon-12 is of use in semiconductors, and the bi-product of this enrichment, Carbon-13 already has known uses in the biomedical field.

3.Silicon- Laser enrichment of silicon can be used for creating advanced semiconductor material. Creating isotopically pure silicon may be of use in devices with semiconductors, which include all computers and electronic devices. These devices that use silicon in its current form are reaching performance limits, and may be able to benefit from enrichment of silicon, though there is little demand for this and no economically sound source has been developed.[ref 2]

Success of LANL of laser enrichment of different elements can be seen in the table below. The different types of Dissociation methods will be described below in the Analysis section.[ref 3]

Commercial Energy

General Electric (GE) currently plans to use the Australian laser enrichment technology (SILEX) to enrich natural UF6 gas in the uranium-235 isotope. GE is planning to conduct the project in two phases. The first, a test phase while the latter being a commercial-scale enrichment plant phase. The Test Loop, which is being built at GE's nuclear fuel fabrication facility in Wilmington, North Carolina, USA, will verify performance and reliability data for full scale (commercial-like) facilities [ref 4]. This change in energy source could prove to be a much cheaper way of energy production that would allow for the lowering of cost per unit of power.

Nuclear Weapons

Fuel for nuclear reactors does not come out of the ground ready to used. Rather, fuel suppliers must process natural uranium to extract small amounts of the rare fissile U-235 isotope to produce the fuel pellets that reactors use to generate power. Typically a power reactor will utilize fuel enriched with 3% U-235, a nuclear weapon 80-90%.

Over the decades efforts continued to develop more economical enrichment techniques for both civil and military purposes. Much research centered on laser enrichment.

The Nuclear Regulatory Commission staff contends that its current licensing suffices to deal with security questions, but APS responds that "nonproliferation is not given an adequate level of attention." It gets support from NRC chairman Gregory Jaczko who conceded in a July 12, 2010 speech that "the smaller footprint and lower energy needs of the laser enrichment technology have been the cause of concern."

While SILEX may still fail as a commercial venture, we must prepare ourselves for success and the renewed interest in laser enrichment it will stimulate globally. With construction of more of the SILEX plant looming, it is none to soon for the Agency to consider interfacing with NRC and GE-Hitachi to work out an arrangement to establish a new safeguard precedent. Clearly marginally tethered international laser development is something we must avoid to prevent yet more nuclear weapons states in the future.[ref 5].

Analysis of SILEX Process

The Separation of Isotopes by Laser Excitation, SILEX,  process exposes a cold stream of a mixture of uranium hexafluoride (UF6) molecules and a carrier gas to energy from a pulsed laser. The laser used is a CO2 laser operating at a wavelength of 10.8 μm (micrometres) and optically amplified to 16 μm, which is in the infrared spectrum. The amplification is achieved in a Raman conversion cell, a large vessel filled with high-pressure para-hydrogen.

The 16 μm wavelength laser preferentially excites the 235UF6, creating a difference in the isotope ratios in a product stream, which is enriched in 235U, and a tailings stream, which has an increased fraction of the more common 238U. In effect, the laser is tuned to electrically charge the U235 atoms, which can become trapped in an electric field and drawn to a metal plate for collection.

According to John L. Lyman, the Silex Systems Ltd. (SSL) research facility in Australia uses a laser pulsed at a frequency of 50 Hz, a rate that results in great inefficiency. At 50 Hz, only 1% of the UF6 feedstock is processed. This results in a high fraction of feedstock entering the product stream and a low observed enrichment rates. Consequently, a working enrichment plant would have to substantially increase the laser duty cycle. In addition, the preparation time needed is prohibitively long for full-scale production. The SSL research facility requires ten hours of prep time for a one-hour enrichment test run, significantly restricting output.[11]

Further details of the technology, such as how it differs from the older molecular laser isotope separation(MLIS) and atomic vapor laser isotope separation (AVLIS) processes are not known publicly and this has been the greatest source of controversy. 

How Laser Enrichment Works

SILEX uses laser radiation to break bonds and ionize elements to separate isotopes by means of selective ionization. For natural uranium in particular, the laser breaks one of the six Florine bonds in UF6 utilizing photo-dissociation to create UF5+ which contains the U-235. Photo-dissociation is a complex process and will be explained below in its own section, but all in all it uses photon interactions with the chemical bonds to break the bonds themselves. The lasers are specifically tuned to ionize U-235, and not U-238.

With the UF5+ which contains U-235 having a positive charge, the molecules can be separated from the UF6 which contains the U-238. The U-235 ions are attracted to and collected on a negatively charged plate. This process can produce samples of nitrogen that are 5% U-235, versus natural uranium which is only 0.7% U-235.[ref 6] Since the energy of a photon is given by the equation:

this shows that the energy is inversely proportional to the wavelength of the photon. Different isotopes have different electronic energies. The equation above shows that energy is a function of wavelength, meaning isotopes of different energies will respond to different color lasers, that have different wavelengths. [ref 8]

Photo-dissociation

Photo excitation of atoms is nothing new. Stanislaw Mrozowski suggested that mercury isotopes might be separated by selective excitation with the 253.7-nanometer resonance line of a mercury arc lamp and subsequent reaction with oxygen. This separation was achieved experimentally by Kurt Zuber in 1935 [ref 3]. In the early 1940s Harold Urey proposed a photochemical method for separating Uranium isotopes but he lost out to the gaseous diffusion technique. After World War II Carbon and oxygen isotopes were also separated by using a strong spectral line of an iodine lamp to excite carbon monoxide molecules. "These pre-laser experiments involved a one step process in which absorbed photons with frequencies in the visible or ultraviolet spectral region to selectively excite electronic states of one isotopic species"[ref 3] 

They were however limited by most molecules having very broad structureless electronic absorptions bands thus making selective excitation by this method impossible and by the intensity of the radiation sources available. Photo-chemical isotope separation requires highly monochromatic, highly intense radiation. High-intensity tunable laser have removed many of the limitations of the early experiments. These laser can be tuned to match any absorption features that show a distinct isotope shift, and because of its high monochromaticity laser light can excite a desired species with reasonable selectivity even when absorption feature of other isotopic species partially overlap those of the desired isotopic species. A high-intensity laser can also saturate the absorbing material as well. 

The best part though is that the laser pulses are short compared with the average time for the selectively excited molecules to lose their energies. Short pulses are needed if the excitation process is to be isotopically selective and efficient in its use of laser photons.

There are three methods of Photo-dissociation that have been used successfully. A single photon process where a visible or an ultraviolet photon excites a molecule to a "predissociative state". A two step process, in which an infrared photon excites a vibrational state of a molecule and an ultraviolet photon dissociates the excited molecule, and a multistep infrared process in which infrared photons excite successively higher and higher vibrational states until the molecule dissociation limit is reached. 

Every one of these processes take advantage that in a vibrational state the nuclei of a molecule undergo oscillatory motion about the ground state configuration at some frequency. This frequency depends on the masses of the nuclei thus the vibrational excitation of a molecule containing a lighter isotope requires absorption of a photon at a higher frequency. This mass dependent shift in the absorption spectrum is exploited to dissociate molecules of one isotopic species selectively to achieve isotope separation.

A single photon excitation relies on predissociation in which a photon induced transition from a bound ground electronic state to an electronic state for which the internuclear forces are always repulsive. The lifetime of such a repulsive state is so short that dissociation follows the transition to the excited state is almost unity probability.

Predissocitation involves a photon-induced transition not directly to a repulsive electronic state but to a predissociative state (a vibrational state within a bound excited electronic state that is energetically coupled to the repulsive electronic state. That is the bound excited and repulsive electronic states have the same energy (the curve-crossing energy) at some internuclear distance greater than the equilibrium internuclear distance for the ground electronic state.) Then if the bound excited and repulsive electronic states have certain symmetry relations and if the energy of the vibrational state is near the curve-crossing energy, dissociation occurs by tunneling from the bound excited electronic state to the repulsive electronic state. This dissociation by tunneling is called predissociation because it requires a photon energy less than that required for dissociation directly from the repulsive electronic state."[ref 3] Tuning a laser to the frequency matching the isotopic species transition energy that species can be selectively excited and dissociated. A requirement for isotopic selectivity of predissociation is that shift of the vibrational energy levels for the different isotopic species be greater than their energy widths.

Los Almos National laboratory has been experimenting using selective photo-dissociation of molecules. Molecules can be excited to dissociate in many different ways, and this is the two step process described above. The two main steps that Los Almos was as follows. The first one was the use of an infrared laser that selectively excites the vibrations of gaseous UF6 that contains the molecule of U-235. As you can see below in part (a) of the figure there is a difference in the energy to excite the vibrational modes of one isotope to another (the solid line is one isotope and the dash line is another isotope.

The arrows in part (a) show the absorption of infrared photons that raise a molecule from the ground state to the first vibrational state. The difference in the lengths of the arrows show the different photon energies, or frequencies needed to excite the two isotopic species but the difference is quite small (less than 1.25X10^-4 eV). 

Monochromatic lasers can achieve selective excitation process though. Part (b) of the diagram shows one of the vibrational transitions in (a) that is split into many rotational states labeled by J (number of rotational angular momentum quanta of the states) At room temperatures molecules populate rotational states with high J values which causes a problem for the monochromatic laser as the laser is tune to excite the ground state to the first vibrational state. If the UF6 are at rotational states above the ground state they will not be excited to the vibrational state and thus you will be unable to dissociate these unexcited molecules. 

Part (b) also shows that during a transition between vibrational states the change in J is restricted to -1, 0, +1 and are denoted as P-, Q-, and R- Branch transitions respectively. You can see in part (c) of the figure above the infrared absorption bands of 235-UF6 and 238-UF6 from 620 to 630 cm^-1 including transition from the ground state to the first excited state of the V3 vibrational mode. The absorptions occur over a broad band of frequencies because molecules in the ground state occupy many rotational states (J) and the molecules in each rotational state can undergo P-, Q-, or R- branch transitions to the first excited vibrational state. As you can see in part (c) the absorption band of 235-UF6 is shifted to slightly higher frequencies relative to that of 238-UF6

An ultraviolet laser is then shot onto the vibrational excited UF6 to dissociate the molecule into UF5 plus a fluorine atom. which cause it to reach the repulsive potential dissocation limted as show in the figure below

Ideally the lower-frequency ultraviolet photons will not dissociate the unexcited molecules and the selectivity of the first step will be preserved. In this process the excitation and dissocation must occur on a time scale that is short compared to the lifetime of the vibrational state otherwise they can undergo collisions and lose their excited vibrational state. We can see the benefit of using the two step process to help improve the selectivity of the isotopes that undergo photo-dissociation by looking ultraviolet dissociation cross section for vibrational excited molecules and unexcited molecules as shown below

As you can see above the dissociation probability as a function of ultraviolet photon frequency of both the excited and unexcited states. Without infrared excitation the dissociation cross-section for different isotopic species are nearly the same. Infrared excitation increase the photo-dissociation cross section at a given frequency and shifts the threshold for dissociation to lower frequencies. This allows you to choose an ultraviolet laser frequency at which the dissociation cross section is large for excited molecules and small for unexcited molecules.

In multiple-photon dissociation they try to make the most of the fact that the threshold frequency for ultraviolet dissociation shifts more and more to the color red as the infrared laser fluence (flux integrated over time) increases. The figure blow shows the ultraviolet dissociation cross section spectrum for CF3I.

These shifts clearly show that the laser is exciting the molecules to very high vibrational states and if molecular vibrations were governed by forces that increased linearly with displacement as if they were a harmonic oscillator the energy difference between vibrational states would be constant and photons with this constant energy could resonantly induce transitions to higher and higher vibrational states. 

Part (a) in the next figure shows the excitation states. Unfortunately most molecular vibrations are anharmonic that is they have nonlinear forces. The anharmonicity cause the energy differences between vibrational states to become smaller and smaller as shown in the figure above in part (b). As the molecules vibrational energy increase it should absorb infrared photons of lower energy and its interacton with constant-energy photons becomes ineffective of exciting it to the next vibrational state. This is the cause of the multi-stage needed for multi-photon dissociation.

A diagram of a proposed system for a multi-photon dissociation system for enriching Uranium enrichment of UF6 gas is shown below.

((All figures from this section was taken from source[ref 3]))

Improvements Over Past Techniques

To be of use in nuclear power uranium must be enriched to Uranium-235. The first enrichment process used was gaseous diffusion of uranium, which involves forcing gaseous uranium through porous membranes which essentially filters through U-235 because it is lighter and diffuses faster than U-238. In each successive chamber the concentration of U-235 to U-238 is slightly higher, but more than a thousand chambers are needed to increase the concentration of U-235 to 3.2% which is required for light water reactors. The next process to be developed, which was more cost effective and is now the main commercial process currently in use, involves the centrifuging of uranium. Gaseous uranium is placed in a centrifuge and the heavier isotope U-238 moves to the outside of the centrifuge and U-235 remains in the center. This process is repeated up to 20 times, which is much less than the 1000 stages used in the diffusion process.[ref 9] Using laser excitation, uranium can be enriched to 5% U-235 after only a few stages of the process, but the centrifugal process would require thousands of stages to achieve these results.

Public View and Concerns

The main worry in developing this technology is that laser enrichment is so space and energy effective, so that those using this technology could go undetected by nuclear inspectors. Experts from the Council on Foreign Relations worry that these facilities could be “hidden in a warehouse,” [Ref 10] as the SILEX process is 75% smaller than current techniques. New facilities would not be able to be easily detected by current observation satellites. [ref 11] 

It is important to note that the risk of proliferation is always present with the emergence of new nuclear techniques, although precautions are of course taken by the US government and the UN to prevent the spread of new technologies.

Summary

Laser enrichments purpose of separating isotopes of elements by the process to produce higher concentrations of specific desired isotopes of a chemical element. This process has the potential to be large contributor to the nuclear power industry and weapon development. Using the unique frequencies which atoms vibrate, a laser tuned to the vibrational frequency of an atom allows for harvesting. Because of technical difficulties translation from the laboratory to the commercial or weapons settings despite the efforts of more than a dozen countries since the 1970s, have impeded further advancements.

References

1. ↑ http://www.imp.kiae.ru/_eng/tehn/tehn_txt.htmf
2. ↑ http://www.silex.com.au/s03_about_silex/s30_1_content.html
3. ↑ ^{3.0 3.1 3.2 3.3 3.4 3.5} http://library.lanl.gov/cgi-bin/getfile?04-01.pdf
4. ↑ http://www.nrc.gov/materials/fuel-cycle-fac/laser.html
5. ↑ http://www.huffingtonpost.com/bennett-ramberg-phd/new-peaceful-nuclear-tech_b_830937.html
6. ↑ https://www.llnl.gov/str/Hargrove.html
7. ↑ http://www.peacetasmania.org/weapons_disarm/U_enrichment/NPT_April05_SILEX_Newman4.jpg
8. ↑ https://www.llnl.gov/str/Hargrove.html
9. ↑ http://www.world-nuclear.org/info/inf28.html
10. ↑ http://world-nuclear.org/info/inf28.html
11. ↑ http://www.abc.net.au/news/stories/2010/04/13/2870904.htm