In 1964, the Irish physicist John Stewart Bell came up with a test to try to establish, once and for all, that the counter-intuitive principles of quantum physics are truly inherent properties of the universe — that the decades-long effort of Albert Einstein and other physicists to develop a more intuitive physics could never bear fruit.
Einstein was deeply disturbed by the randomness at the core of quantum physics — "God does not play dice,” as he famously wrote to the physicist Max Born in 1926.
In 1935, Einstein, together with his colleagues Boris Podolsky and Nathan Rosen, described a strange consequence of this randomness, now called the Einstein, Podolsky, Rosen (EPR) Paradox.
According to the laws of quantum physics, it is possible for two particles to interact briefly in such a way that their states become “entangled” as “EPR pairs.” Even if the particles then travel many light years away from each other, one particle somehow instantly seems to “know” the outcome of a measurement on the other particle: When asked the same question, it will give the same answer, even though quantum physics says that the first particle chose its answer randomly. Since the theory of special relativity forbids information from traveling faster than the speed of light, how does the second particle know the answer?
To Einstein, this “spooky action at a distance” implied that quantum physics was an incomplete theory. “Quantum mechanics is certainly imposing,” he wrote to Born. “But an inner voice tells me that it is not yet the real thing.”
Over the remaining decades of his life, Einstein searched for a way that the two particles could use classical physics to come up with their answers — hidden variables that could explain the behavior of the particles without a need for randomness or spooky actions.
But in 1964, Bell realized that the EPR paradox itself could be used to devise an experiment that determines whether quantum physics or a local hidden-variables theory correctly explains the real world.
The Bell Test experiment, is one which can be adapated into a diverse range of algorithms and strategies which can be implemented with experimental equipment.
Let us examine one such strategy with a game. Let us say this takes place in a universe where everyone is a physicist, even thieves and police detectives! But this is the 1930's and their is prohibition against using quantum mechanics! :)
In this we have 2 thieves, Bonnie and Clyde, who are separately questioned by a detective in separate rooms after they were captured following a robbery of a physics lab and car chase.
Their joint goal is to give either identical answers or different answers, depending on what questions the detective asks them. Neither player knows what question the detective is asking the other player.
The questions given to the two of them are either a A or B, chosen randomly.
Bonnie and Clyde each answer by giving the detective an answer X or Y.
If either player (or both) received a A, they must hand in matching X's or Y's to win.
But if both players got a B, they must hand in X+Y or Y+X to win.
Classically, this is represented by the familiar "prisoner's dilemma" from game theory where, under questioning:
Answer X = remain silent
Answer Y = confess
Bonnie and Clyde were questioned in separate rooms, and each was offered the same deal by the detective. The deal went as follows (since both are the same, we need only describe the version presented to Bonnie):
``Bonnie, here's the offer that we are making to both you and Clyde. If you both hold out on us, and don't confess to bank robbery, then we admit that we don't have enough proof to convict you. However, we will be able to jail you both for 1 year, on the count of reckless driving.
If you turn state's witness and help us convict Clyde (assuming he doesn't confess), then you will go free, and Clyde will get 20 years in prison. On the other hand, if you don't confess and Clyde does, then he will go free and you will get 20 years.''
``What happens if both Clyde and I confess?'' asked Bonnie.
``Then you both get 5 years,'' said the detective.
The possible strategies can be seen, in the graphical payoff table
Using the game table, we see right away that the worst strategy is for them both to give different answers to each other. Hence the only viable strategy is for Bonnie and Clyde to decide, in a contingency plan before they were captured, that under such interrogation they will simply remain silent, i.e. both give the same answer X, no matter what random question, A or B, the detective asks them.
Since the detective is asking them questions as a part of a random basis, A or B, Bonnie and Clyde have shared random outcomes, X or Y. Hence we can forget that the detective even exists and instead construct A and B can as basis elements of a random 0 or 1 outcome, which Clyde and Bonnie share between them.
Using this we can construct the following truth table
This is the same logic table for an AND gate.
Which shows us that, employing this strategy, this will give them
75% chance of winning.
If Bonnie and Clyde have only classical physics at their disposal, it turns out that this is the best they can do.
But Bonnie and Clyde can significantly increase their chance of winning if they had stolen an EPR quantum entangled pair of particles. This is exactly what they did before they were captured! The players can now agree ahead of time that after the detective hands them their questions, they will measure their particles in carefully chosen ways to gain an advantage over classical probability rules.
The most general possible state of the system is a superposition of amplitudes α and β
where
so that the state has unit probability.
two entangled qubits in the Bell state
In this state, called an equal superposition, there are equal probabilities of measuring either 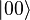 or
or 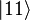 , as
, as
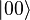 or
or 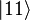 , as
, as .
.In the case of a two-strategy game this can be physically implemented by the use of an entity like the electron which has a superposed spin state, with the base states being +1/2 (plus half) and −1/2 (minus half). The two basis states in this system denote the amplitudes for the object to have the component of its spin in the z-axis of the complex plane to be equal to + ħ/2 and - ħ/2 respectively.
The possible states for a single qubit can be visualised using a Bloch sphere.
Represented on such a sphere, a classical bit could only be at the "North Pole" or the "South Pole", in the locations where
 and
and  are respectively.
are respectively. The rest of the surface of the sphere is inaccessible to a classical bit, but a pure qubit state can be represented by any point on the surface. For example, the pure qubit state
 would lie on the equator of the sphere, on the positive y axis.
would lie on the equator of the sphere, on the positive y axis.A singlet made from two spin-1/2 objects has a wave function which is a superposition of the form
This is an entangled state; a measurement of the component of the spin in any direction for the first object will give either up or down with probability 1/2 each and will automatically imply that a measurement of the spin in the same direction for the second object will give the opposite value
(down or up)
More generally, if Bonnie measures the component of the spin in a particular direction and finds some value, and Clyde measures the spin in some other direction which is at an angle θ with respect to the first direction, then Clyde will find the opposite value of the spin with a computable probability to generate an optimum payoff.
To compute the probability, Clyde uses a direction in the polar coordinatess (θ, φ) (θ is the angle between this direction and the z-axis), where the wave function of a spin-1/2 object whose spin component in that direction is given by ħ/2 is
given by the amplitudes
 and
and 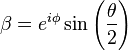 .
.where
 is the angle from the z-axis and
is the angle from the z-axis and  is the azimuthal angle on the Bloch Sphere. The Bloch vector precesses about the z-axis.
is the azimuthal angle on the Bloch Sphere. The Bloch vector precesses about the z-axis.From this one can show that if one of the two objects in a singlet has its spin pointing along the
z-axis, the probability (the amplitudes squared) that the spin of the other object will point in the same direction as (or opposite to) (θ, φ) is given by
The above facts motivate the following quantum strategy map for Bonnie and Clyde to work with:
Where α, β, γ are quantum amplitudes. The four directions are taken to lie in a plane with relative amplitudes between them as shown
Going back to the game model and using our new quantum strategy map, if Bonnie is asked question A/B at random, she measures the spin of her spin-1/2 object in the direction indicated by amplitudes β and γ
Meanwhile, if Clyde is asked the question A/B at random, he measures the spin of his
spin-1/2 object in the direction indicated by amplitudes α and β
In all cases, Bonnie and Clyde both answer X (remain silent) if they find the component of their spin to be + ħ/2, and Y (confess) if the spin component is - ħ/2.
Each of the spin states can be used to represent each of the two strategies available to the players. When a measurement is made on the electron, it collapses to one of the base states, thus conveying the strategy used by the player.
The measurements are designed to produce a high chance of identical results when at least one of the players receives an A, and a high chance of opposite results when the players both get Bs. If they follow this strategy, their expected pay-off in the long run is given by
Note: The factor of 1/4 is because Bonnie and Clyde are asked questions randomly, i.e. with probability 1/2 between each of them.
Maximising this expression with respect to quantum amplitudes α, β, γ gives
α=β=γ=π/4,
Winning pairs
are at angle π/8
Losing pairs are at angle 3π/8
and the expected optimum pay-off is that they can win with probability
P = cos^2(π/8) = 0.8536 = 85.36%
if they follow the quantum strategy, compared to the 75% chance by the classical strategy.
We can therefore test if the message has been read before it reaches the intended recipient - something that is impossible using classical signals. This in a sense can gives us security in the same way that it gave Bonnie and Clyde the ability to trick the detective in the example above.
By "breaking the law" within the classical probabilistic strategy of investigation, Bonnie and Clyde have a 10.36% advantage over their classical investigator proving once again that quantum physics does pay!









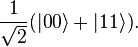







No comments:
Post a Comment
Note: only a member of this blog may post a comment.