Quantum Encryption of Images in Python using Bitwise XOR and a QRNG

XOR Cipher in Standard Cryptography

In Cryptography, the exclusive OR or XOR Cipher is an additive method of encryption of a string of data using a particular key.

The XOR operator is extremely common as a component in more complex ciphers. By itself, using a constant repeating key, a simple XOR cipher can trivially be broken using frequency analysis for pattern recognition as a means to reconstruct the key generation process, if not made using a Pseudo-Random Number Generator for instance. If the content of any message can be guessed or otherwise known then the key can be revealed.

The primary merit of the XOR Cipher is that it is simple to implement, with the XOR operation being computationally inexpensive. 

The XOR Cipher itself can be implemented using a XOR Logic Gate in a Bitwise Function.

an encryption algorithm that uses the XOR operates according to the principles:

A ${\displaystyle \oplus }$ 0 = A,

A ${\displaystyle \oplus }$ A = 0,

A ${\displaystyle \oplus }$ B = B ${\displaystyle \oplus }$ A,

(A ${\displaystyle \oplus }$ B) ${\displaystyle \oplus }$ C = A ${\displaystyle \oplus }$ (B ${\displaystyle \oplus }$ C),

(B ${\displaystyle \oplus }$ A) ${\displaystyle \oplus }$ A = B ${\displaystyle \oplus }$ 0 = B,

where ${\displaystyle \oplus }$ denotes the exclusive OR (XOR) logic operation. This operation is sometimes called modulus 2 addition (or subtraction, which is identical). With this logic, a string of text can be encrypted by applying the bitwise XOR operator to every character using a given key. 

To decrypt the output, merely reapplying the XOR function with the key will remove the cipher, as the XOR operation is its own inverse.

In any of these ciphers, the XOR operator is vulnerable to a known-plaintext attack, since 

plaintext  ciphertext = key.

If the key used is random, then the XOR operation will in a sense preserve the randomness of the key in the encrypted data. The result is a random stream cipher. If a key is generated using a truly random number source, such as a quantum random number generator, the result is the generation of one-time pad using a single use, truly unique key that is in principle impossible to crack. This is the motivation for generating QRNGs which can combat the emergence of quantum computation that could, in principle, perform known-plaintext attacks of stream cipher encryption in polynomial time. Quantum Encryption is the only known way to combat this threat.

We can examine 2 methods to create encryption keys: using a Quantum Random Number Generator and by Using quantum correlated images captured using entangled photons.

Quantum Random Number Generation

As previously discussed, the random stream XOR cipher can be generated using a random number generator. pseudo-random number generators (PRNGs) are build on algorithms involving some kind of recursive method starting from a base value that is determined by an input called the "seed". The default PRNG in most statistical software (R, Python, Stata, etc.) is the Mersenne Twister algorithm MT19937, which is set out in Matsumoto and Nishimura (1998). This is a complicated algorithm, so it would be best to read the paper on it if you want to know how it works in detail. In this particular algorithm, there is a recurrence relation of degree n$n$, and your input seed is an initial set of vectors x0,x1,...,xn−1${\mathbf{x}}_0,{\mathbf{x}}_1,...,{\mathbf{x}}_{n-1}$. The algorithm uses a linear recurrence relation that generates:

xn+k=f(xk,xk+1,xk+m,r,A),$${\mathbf{x}}_{n+k}=f({\mathbf{x}}_k,{\mathbf{x}}_{k+1},{\mathbf{x}}_{k+m},r,\mathbf{A}),$$

where 1⩽m⩽n$1⩽m⩽n$ and r$r$ and A$\mathbf{A}$ are objects that can be specified as parameters in the algorithm. Since the seed gives the initial set of vectors (and given other fixed parameters for the algorithm), the series of pseudo-random numbers generated by the algorithm is fixed. If you change the seed then you change the initial vectors, which changes the pseudo-random numbers generated by the algorithm. This is, of course, the function of the seed.

Now, it is important to note that this is just one example, using the MT19937 algorithm. There are many PRNGs that can be used in statistical software, and they each involve different recursive methods, and so the seed means a different thing (in technical terms) in each of them. You can find a library of PRNGs for R in this documentation, which lists the available algorithms and the papers that describe these algorithms.

The purpose of the seed is to allow the user to "lock" the pseudo-random number generator, to allow replicable analysis. Some analysts like to set the seed using a true random-number generator (TRNG) which uses hardware inputs to generate an initial seed number, and then report this as a locked number. If the seed is set and reported by the original user then an auditor can repeat the analysis and obtain the same sequence of pseudo-random numbers as the original user. If the seed is not set then the algorithm will usually use some kind of default seed (e.g., from the system clock), and it will generally not be possible to replicate the randomisation.

Using a Quantum random number source allows for much greater security as we can create numbers that are irreducibly random. Using a quantum-entanglement photon source based on the Beta-Barium Borate non-linear crystal, we can configure photo detectors that can detect the H and V modes of pair of entangled 810nm photons, These photons will be in superposition until the moment they are detected and so will represent the perfect 50/50 coin toss.  

The setup is showcased in the following video:

Entangled Photon Imaging

The diagram below showcases the scheme for quantum encryption using images of entangled photons processed using bitwise XOR on any image we want to encrypt using a shared quantum key distrubted between 2 users, Alice and Bob. 

Each recipient recieves the relative  anti-correlations to each other and so can encrypt or decrypt their transferred image in a one time pad use.

using a CCD with a large enough sensor we can image pairs of entangled photons at 810nm using a narrow single-band pass filter at around 800-830nm

Quantum image encryption and decryption

Images contain information in both the form of metadata on the conditions the image was captured and in the pixel data itself. Metadata can be encrypted as a data stream so we will refer to image encryption as encryption of the pixel information itself from this point.

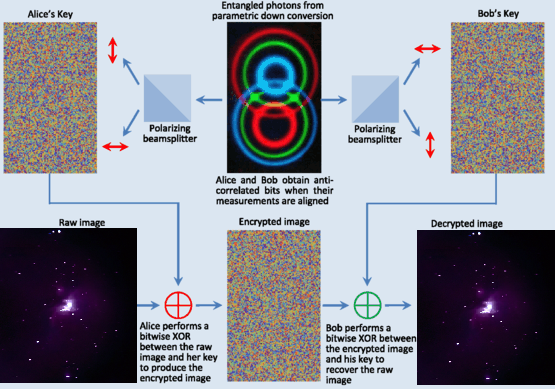
The definition of image encryption is an extension of data encryption in general: through the bitwise XOR operation of the original image pixels and the key image pixels, with the key image being either a pseudo-random stream cipher or the quantum random stream cipher or anti-correlated entangled information shared over a secure channel.

In either case we Perform bitwise XOR operation on the encrypted image and the key image.

It can be seen from the image encryption and decryption that they are all the same operation.

We now stipulate that the literal symbol of XOR is xor. According to the above bitwise XOR operation, we assume:

xor(a,b)=c

You can get:

xor(c,b)=a

Or:

xor(c,a)=b

In summary, we assume that a is the original image data and b is the key, then c calculated by xor(a,c) is the encrypted ciphertext. 

In summary:

Encryption process: Perform a bitwise XOR operation on the image a and the key b to complete the encryption and obtain the ciphertext c.

Decryption process: Perform a bitwise XOR operation on the ciphertext c and the key b, complete the decryption, and get the image a.

We can use our quantum random numbers generator in 2 ways to create our image encryption key:

(1) as a random number generator seed source

(2) using the random superposition of the H and V modes

We can also use the shared set of correlated images, captured using the single CCD, from our entangled photon source with Alice getting one half and Bob getting the anti-correlated half. This provides the perfect key, with the quantum images shared over a separate channel hidden from the encrypted classical images.

The file exchange channel is 2 way:

Alice can use Her key to encrypt the image, Bob can use His key to decrypt the image

OR

Bob can use His key to encrypt the image, Alice can use Her key to decrypt the image.

The XOR Cipher in this use can also be extended as a component in more complex overlay network ciphers if need be however for computational efficiency it is not necessary. It is just as effectual to have 1 quantum cipher as many, so in effect the system is completely hidden, by virtue of hidden variables, and is encrypted in an information condensate.

We can use my suite of image analysis plots to perform histogram analysis and construct a correlogram to try and do a routine check to see if the image encryption could be vulnerable to frequency analysis from the encrypted image pixel data:

Afterward:

Encryption of information, in particular visual information in the form of images and video, is of ever increasing importance online. Encryption of image metadata can be accomplished in tandem with encryption of pixel data to make for a more robust as well as computational inexpensive process using the XOR cipher combined with quantum RNGs and anti-correlated quantum information generated via entanglement sources. 

Research is also ongoing to use a variety of different entanglement sources, both optical (using Non-linear crystals) and in the Microwave Domain (using Josephson Junctions) with the goal being a many spectrum approach to secure information transfer. 

This would allow, among other things a secure, quantum entangled channel transferring the anti-correlated entangled key to operate on a separate band from the wavelengths used to generate the entangled key for instance. 

Moreover although line-of-sight optical communication has had much fanfare it sees that the microwave band still offers superior connectivity in telecoms infrastructure and will most likely be the focus of further generations of secure data transfer in mobile applications. Quantum Encryption therefore is a key niche in this area and XOR-based ciphers will be the fastest to implement in terms of wireless/non-fiber secure quantum communication. 

 

Github Files:

https://github.com/MuonRay/Quantum-Encryption-of-Images-using-Bitwise-XOR-and-QRNG